Problemas – Rotações – Prof. F. Sato

http://www.fisica.ufjf.br/~sjfsato/fisica1

[1] Considere três massas dispostas em um plano como na figura abaixo, com o eixo de rotação perpendicular ao plano e passando por P. (a) Qual o valor do momento de inércia desse sistema? (b) Se o sistema tiver uma velocidade angular (ω), quanto vale a energia cinética de rotação?

[2] Dada a figura abaixo qual o valor de x que minimiza o momento de inércia? Mostre que , sendo que e x_cm é o valor de x calculado anteriormente.

[3] Um método tradicional para medir a velocidade da luz utiliza uma roda giratória. Um feixe de luz passa pelo espaço livre entre dois dentes situados na borda da roda, como na figura abaixo, viaja até um espelho distante e chega de volta exatamente a tempo de passar pelo espaço seguinte entre dois dentes.. Uma dessas rodas tem 5.0 cm de raio e 500 espaços entre dentes. Medidas realizadas quando o espelho está a uma distância L=500 m da roda fornecem um valor de 3,0x10⁵ km/s para a velocidade da luz. (a) Qual é a velocidade angular (constante da roda)? (b) Qual é a velocidade linear de um ponto na borda da roda?

[4] Uma chaminé cilindrica começa a tombar quando sua base é danificada. Trate a chaminé como uma barra fina de comprimento L. (a) Qual a velocidade angular ω da chaminé em função do ângulo ? (b) Qual a aceleração radial a_r? (c) Qual a aceleração tangencial a_T?

[5] Uma casca esférica uniforme de massa M e raio R pode girar em torno de um eixo vertical sem atrito (conforme a figura abaixo. Uma corda de massa despresível esta enrrolada no equador da casca, passa por uma polia de momento de inércia I e raio r e está presa a um pequeno objeto de massa m. Não há atrito no eixo da polia e a corda não escorrega na casca nem na polia. Qual é a velocidade do objeto depois de cair de uma altura h após ter sido liberado a partir do repouso? (dica: use considerações de energia).

[6] Uma barra fina uniforme de comprimento L e Massa M, articulada em um dos extremos como mostrado na figura é colocada horizontalmente e em seguida abandonada do repouso. Admitindo que a articulação não tem atrito, encontre:

(a) a velocidade angular da barra quando encontra a sua posição vertical; (b) a força exercida pela articulação neste momento; (c) qual a velocidade angular necessária para a barra alcançar a posição vertical no topo desse balanço?

[7] Um disco com 0,5 m de raio e 20 kg de massa gira livremente em torno de um eixo horinzontal fixo passando pelo seu centro. Aplica-se-lhe uma força de 9,8 N puxando-se um fio enrolado em sua borda. Dertemine a aceleração angular do disco e sua velocidade angular após 2s.

[8] Considerando o problema [7] agora consideremos uma situação como a figura abaixo com uma massa mg pendurada. Qual o valor da aceleração angular e aceleração linear?

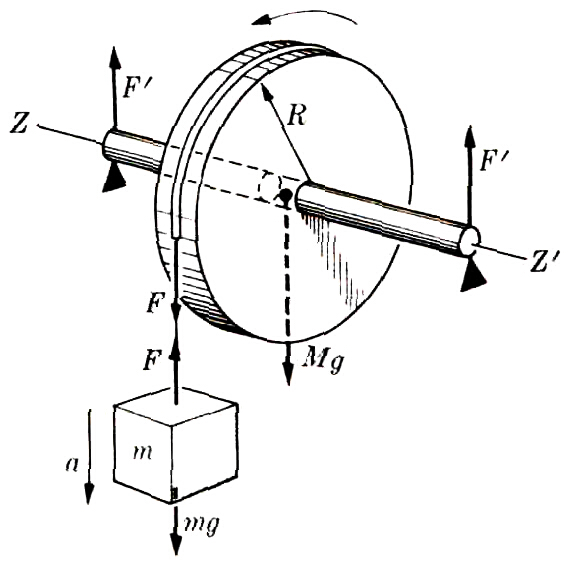
[9] Da figura abaixo, determine a aceleração angular do disco.

[10] Máquina de Atwood, polia com massa. Considere a figura abaixo onde M₁>M₂, a polia com massa M₃ e raio R. Dado que o momento de inércia do disco é dado por escreva as equação das resultantes das forças para o sistema.

[11] Problema de Rolamento no Plano: Considere um disco de espessura uniforme (m = 170 kg), cuja velocidade do centro de massa v_cm = 343 m/s. Qual a energia cinética desse disco?

[12] Rolamento no plano inclinado sem deslizamento: Suponha um corpo de massa M e raio R, rolando suavemente ao longo do eixo x. A rampa é inclinada de um ângulo . Qual a aceleração do centro de massa (a_cm,x)?

[13] Considere que uma barata esteja na extremidade de um disco de raio R.

O disco e a barata estão girando com velocidade angula ω_i. A barata então se desloca para uma posição em direção ao centro de rotação (R/2). (a) Qual a velocidade angular ω_f do sistema? (b) Qual a razão entre a energia cinética final e inicial do sistema?

[14] Rolo compressor: Considere um rolo compressor de massa M, raio R, que está sendo puxado por uma força F. (a) Mostre que aceleração do centro de massa é dado por . (b) Qual é a força necessário para que o bloco na deslize no chão? (c) Qual o mínimo coeficiente de atrito?